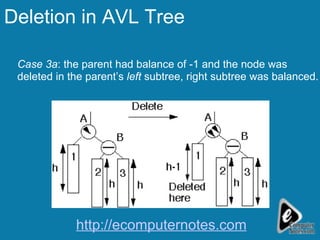
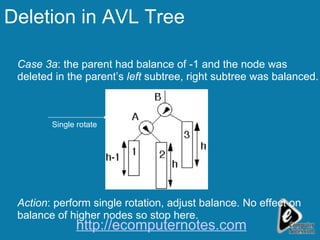
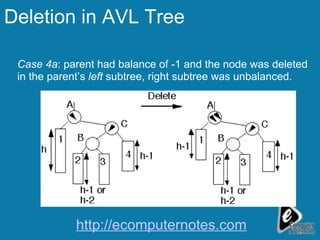
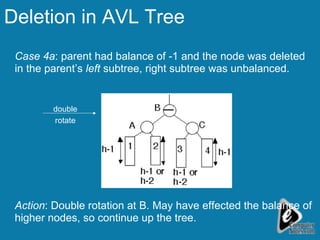
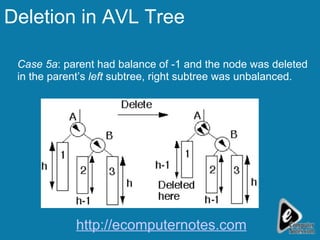
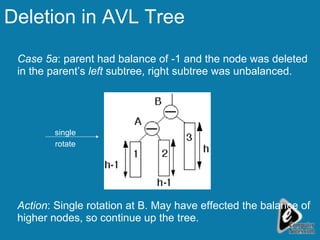
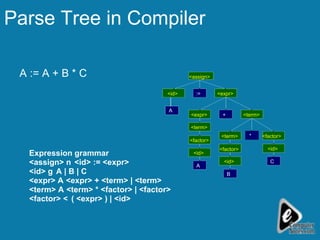
The document discusses deletion in AVL trees and outlines 5 cases to consider when deleting nodes from an AVL tree. It also discusses expression trees and parse trees, providing examples of an expression tree for a mathematical expression and a parse tree for an SQL query. Other uses of binary trees mentioned include their use in compilers for expression trees, parse trees, and abstract syntax trees.

1. Class No.22 Data Structures http://ecomputernotes.com

2. Deletion in AVL Tree There are 5 cases to consider. Let us go through the cases graphically and determine what action to take. We will not develop the C++ code for deleteNode in AVL tree. This will be left as an exercise. http://ecomputernotes.com

3. Deletion in AVL Tree Case 1a : the parent of the deleted node had a balance of 0 and the node was deleted in the parent’s left subtree. Action : change the balance of the parent node and stop. No further effect on balance of any higher node. Delete on this side http://ecomputernotes.com

4. Deletion in AVL Tree Here is why; the height of left tree does not change. 1 2 3 4 5 6 7 0 1 2 http://ecomputernotes.com

5. Deletion in AVL Tree Here is why; the height of left tree does not change. 1 2 3 4 5 6 7 2 3 4 5 6 7 0 1 2 remove(1) http://ecomputernotes.com

6. Deletion in AVL Tree Case 1b : the parent of the deleted node had a balance of 0 and the node was deleted in the parent’s right subtree. Action : (same as 1a ) change the balance of the parent node and stop. No further effect on balance of any higher node. Delete on this side http://ecomputernotes.com

7. Deletion in AVL Tree Case 2a : the parent of the deleted node had a balance of 1 and the node was deleted in the parent’s left subtree. Action : change the balance of the parent node. May have caused imbalance in higher nodes so continue up the tree. Delete on this side http://ecomputernotes.com

8. Deletion in AVL Tree Case 2b : the parent of the deleted node had a balance of -1 and the node was deleted in the parent’s right subtree. Action : same as 2a: change the balance of the parent node. May have caused imbalance in higher nodes so continue up the tree. Delete on this side http://ecomputernotes.com

9. Deletion in AVL Tree Case 3a : the parent had balance of -1 and the node was deleted in the parent’s left subtree, right subtree was balanced. http://ecomputernotes.com

10. Deletion in AVL Tree Case 3a : the parent had balance of -1 and the node was deleted in the parent’s left subtree, right subtree was balanced. Action : perform single rotation, adjust balance. No effect on balance of higher nodes so stop here. Single rotate http://ecomputernotes.com

11. Deletion in AVL Tree Case 4a : parent had balance of -1 and the node was deleted in the parent’s left subtree, right subtree was unbalanced. http://ecomputernotes.com

12. Deletion in AVL Tree Case 4a : parent had balance of -1 and the node was deleted in the parent’s left subtree, right subtree was unbalanced. Action : Double rotation at B. May have effected the balance of higher nodes, so continue up the tree. rotate double

13. Deletion in AVL Tree Case 5a : parent had balance of -1 and the node was deleted in the parent’s left subtree, right subtree was unbalanced. http://ecomputernotes.com

14. Deletion in AVL Tree Case 5a : parent had balance of -1 and the node was deleted in the parent’s left subtree, right subtree was unbalanced. Action : Single rotation at B. May have effected the balance of higher nodes, so continue up the tree. rotate single

15. Other Uses of Binary Trees Expression Trees http://ecomputernotes.com

16. Expression Trees Expression trees , and the more general parse trees and abstract syntax trees are significant components of compilers. Let us consider the expression tree. http://ecomputernotes.com

17. Expression Tree (a+b*c)+((d*e+f)*g) a c + b g * + + d * * e f http://ecomputernotes.com

18. Parse Tree in Compiler Expression grammar <assign>  <id> := <expr> <id>  A | B | C <expr>  <expr> + <term> | <term> <term>  <term> * <factor> | <factor> <factor>  ( <expr> ) | <id> <assign> <id> <expr> <expr> <term> <term> <term> <factor> C B * + <id> <id> A := A <id> <factor> <factor> A := A + B * C

19. Parse Tree for an SQL query Consider querying a movie database Find the titles for movies with stars born in 1960 The database has tables StarsIn(title, year, starName) MovieStar(name, address, gender, birthdate) SELECT title FROM StarsIn, MovieStar WHERE starName = name AND birthdate LIKE ‘%1960’ ; http://ecomputernotes.com

20. SQL Parse Tree < Query > SELECT <SelList> FROM <FromList> WHERE <Condition> <Attribute> <RelName> , <FromList> AND title StarsIn <RelName> <Condition> <Condition> <Attribute> = <Attribute> <Attribute> LIKE <Pattern> starName name birthdate ‘%1960’ MovieStar http://ecomputernotes.com

21. Compiler Optimization Common subexpression: (f+d*e)+((d*e+f)*g) f e + d g * + + d * * e f http://ecomputernotes.com

22. Compiler Optimization (Common subexpression: (f+d*e)+((d*e+f)*g) f e + d g * + * Graph! http://ecomputernotes.com